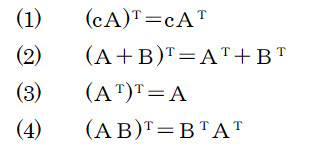数学的準備
1.ベクトル
物体の位置,速度,加速度,角速度,角加速度 いずれも3次元空間のベクトルとして表現できる。 ベクトルは一般に大きさと向きを持った量であり,特に向きを定量的に表現しようとする場合,座標系を定義する必要が生じる。
座標系は 3つの独立したグランド基底ベクトルの組で規定される。 例えば,基底ベクトルをa1,a2,a3とする場合,任意のベクトルは,
X = x1a1+ x2a2 +x3a3 (1.1)
と表現できる。,ここで,x1,x2,x3は基底ベクトル a1,a2,a3を用いたときのベクトルxの座標成分と呼ばれる。 さらに
{a}T = {a1,a2,a3} (1.2)
X = [x1,x2,x3]T (1.3)
を定義することで,(1.1)式は形式的に次のように書き換えられる。
X = {a}T x (1.4)
ベクトルの座標成分で構成されるxは,数学一般の定義と異なりベクトルとは呼ばずに3行1列の行列とみなされる。 xをベクトルxの行列表現と呼ぶ。xは3×1の列行列であり,座標系の選び方によって値が変わるものであるから,ベクトルxとは区別される。また,{a}をベクリックスやベクトル配列という呼び方をする場合もある。 明らかに以下の関係が成立する。
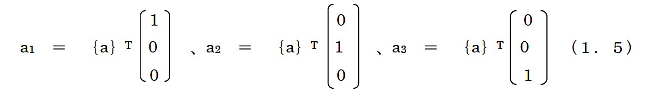
2.ダイアディック
(1.1)式において,任意のベクトルは基底ベクトルの線形結合として表現できるが,この拡張として,基底ベクトルの2次形式のダイアディックが定義できる。 基底ベクトルをa1,a2,a3として
![]()
のように書き表される。 あるいは,3行3列の行列X={xij}を用いて
X={a}T X {a} (1.7)
のように書き換えられる。 (1.4)式でベクトル x そのものは座標系の取り方とは無縁のものであるが,行列 x は座標のとり方に依存して決まる量であったのと同様に, (1.7)式でダイアディックXそのものは座標の座標系の取り方とは無縁であるが,行列Xは座標系のとり方に依存して決まる量である。
3.代数演算
任意のベクトルを x,y とする。 これらの同一の正規直交基底ベクトル{a}に対する座標をそれぞれ,x=[x1 x2 x3]T
y=[y1 y2 y3]Tとする。
すなわち,
x = {a}Tx = {a}T[x1 x2 x3]T
y = {a}Ty = {a}T[y1 y2 y3]T
また,任意のダイアディックDは,次式で記述されるものとする。

4.内積
x,yの内積(スカラー積)は次式で定義される。![]()
ベクトルの内積によってスカラーが得られる。
また,ベクトル配列によっても以下のような内積を定義する。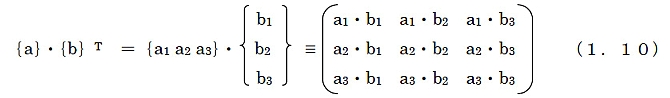
ベクトル配列の内積によって行列が得られる。
内積の定義により
![]()
が成り立つ。 また正規直交基底ベクトルの性質として![]()
が成り立つ。 但し、U33は3次の正方行列正方行列である。
また,ダイアディックとベクトルの内積についても以下のように定義する。
![]()
例)
任意のベクトル v との内積が元のベクトル v となるようなダイアディック U33![]()
を単位ダイアディックという。
5.外積
x,yの外積は次式で定義される。![]()
ただし,演算子(~)は任意の3行1列の行列 z =[z1 z2 z3]Tに作用して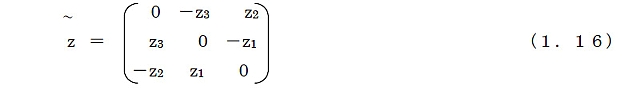
の歪対称行列(反対称行列)を得るものである。 ベクトルの外積によってベクトルが得られる。 また,ベクトル配列についても以下のように外積を定義する。
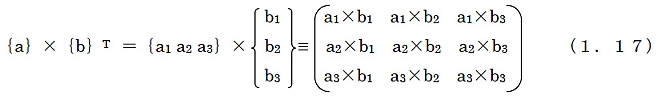
6.ノルム
xのユークリッドノルムは次式で定義される。
![]()
8.定義 (転置行列) aijを (i,j)成分とする(m,n)型の行列A=(aij)に対して,ajiを(i,j)成分とする(n,m)型の行列をAの転置行列(transposed matrix)といい,AT,またはtAで表す。
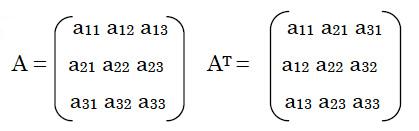
命題 転置行列について次の関係が成り立つ。