| 1数学的基礎 |
| (a)オイラーの回転軸 |
| (b)方向余弦行列 |
| 例 |
| 2.応用編 |
| フレームマトリックス法 |
| 2:座標変換 (a)オイラーの回転軸 任意の基準座標系をA,ある剛体に固定された座標系をBとする。 AとBの両者に固定されたある軸のまわりにBを回転させることで,剛体を任意の姿勢に変更できる。 逆に言うと,回転前後の姿勢が与えられたとするとき,これを関連付ける回転軸が唯一定まる。 これをオイラー軸と呼び,またこのような定理を回転に関するオイラーの定理という。 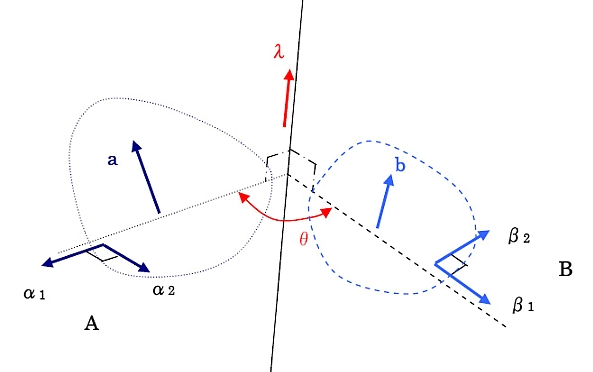 Aに固定された任意のベクトルをa, Bを回転させる前の状態においてaと一致し,Bに固定されたベクトルをb,オイラーの回転軸をλ,その軸のまわりの回転角をθとするとき, 次の式が成り立つ。 b=acosθ−a×λsinθ+a・λλ(1−cosθ) (2.1) また,回転ダイアディック C=U33cosθ−U33×λsinθ+λλ(1−cosθ) (2.2) を定義すれば, (2.1)式は次のように書き換えられる。 b=a・C (2.3) 導出: A系に固定されたベクトルα,αを考え,と組で {α α }が正規直交基底をなすものとする。 B系に固定されたベクトルβ,βを考え,と組で {β β }が正規直交基底をなすものとする。ただし,B系を回転させる前の状態において,β,β は,それぞれα,αと一致するものとする。 すなわち,θ=0において,あるスカラー量p1,p2,p3を用いて, a = p1α+p2α+p3 (2.4) b = p1β+p2β+p3 (2.5) が成り立つ。一方 回転後のβ,βは,α,αの線形結合として 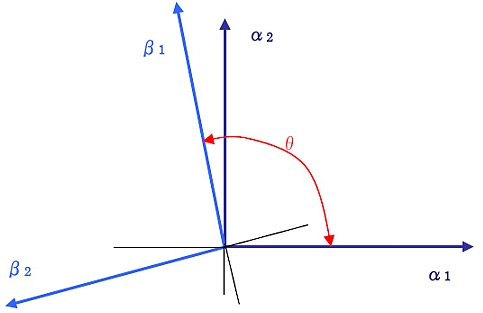 β = cosθα+cos(θ−π/2)α= cosθα+sinθα (2.6) β = cos(θ+π/2)α+cosθα=−sinθα+cosθα (2.7) として書き表される。 従って, b = p1(cosθα+sinθα)+p2(−sinθα+cosθα)+p3 = (p1cosθ−p2sinθ)α+(p1sinθ+p2cosθ)α+p3 (2.8) また,は次のように展開できる。 a・C = acosθ−a×λsinθ+a・λλ(1−cosθ) =(p1α+p2α+p3)cosθ−(p1α+p2α+p3)×sinθ +(p1α+p2α+p3)・λλ(1−cosθ) =p1cosθα+p2cosθα+p3cosθλ+p1sinθα−p2sinθα+p3λ−p3cosθλ =(p1cosθ−p2sinθ)α+(p1sinθ+p2cosθ)α+p3 (2.9) 従って, b = a・C (2.10)
(b)方向余弦行列 任意の2つの正規直交座標ベクトルを{a}T={a1 a2 a3},{b}T={b1 b2 b3}とするとき,方向余弦と呼ばれる9つのスカラー量は Cij=ai・bj (i,j=1,2,3) (2.11) により定義する。 このとき, {b}T = {a}T ACB (2.12) {a}T = {b}T (ACB)T (2.13) が成り立つ。 ただし  これを,{b}から{a}への方向余弦行列あるいは座標変換行列という。 方向余弦行列の性質として,以下のようなものがある。 C−1 = CT (2.15) C CT = CTC = U33 (2.16) (BCA)−1 = (BCA)T = ACB (2.17) 方向余弦行列により,異なる基底ベクトルに対する座標成分の変換が行われる。例えば,任意のベクトル r の{a}系での座標を Ar = [Ar1 Ar2 Ar3]T (Ari = r・ai (i=1,2,3)),{b}系での座標を Br = [Br1 Br2 Br3]T (Bri = r・ai (i=1,2,3))とすれば, Br = Ar ACB (2.18) が成り立つ。 同様に,任意のダイアディックDの{a}系に対応する正方行列を AD (ADij = ai・D・aj (i,j=1,2,3), {b}系に対する正方行列を BD (ADij = bi・D・bj (i,j=1,2,3),とすれば, BD = (ACB)T AD ACB (2.19) が成り立つ。 A系からB系への方向余弦行列を ACB ,A系からB’系への方向余弦行列を ACB’ ,B’系からB系への方向余弦行列を B’CB とするとき,次式が成り立つ。 ACB = ACB’ B’CB (2.20) 例 グランドに固定されたグランド座標系をAとする。 移動するラグビーセンサのセンサシステム上のセンサー座標をBとする。 このとき,B上で計算された任意のベクトル b (例:加速度aおよび角速度ω)は,A座標系上のベクトルaとの関係式として次のように表される。 bi = ai・C (i=1,2,3) a=(a1,a2,a3) Cij = ai・bj = ai ・(aj・C) (i,j=1,2,3) Cij = ai・(aj cosθ−aj×λsinθ+λλ・aj(1−cosθ)) = ai・aj cosθ−ai・(aj×λ)sinθ+ai・λλ・aj(1−cosθ)) λi = λ・ai = λ・bi (i=1,2,3) C11= cosθ+ λ12(1−cosθ) C12=−λ3sinθ+λ1λ2(1−cosθ) C13= λ2sinθ+λ1λ3(1−cosθ) C21= λ3sinθ+λ2λ1(1−cosθ) C22= cosθ+ λ22(1−cosθ) C23=−λ1sinθ+λ2λ3(1−cosθ) C31=−λ2sinθ+λ3λ1(1−cosθ) C32= λ1sinθ+λ3λ2(1−cosθ) C33= cosθ+ λ32(1−cosθ) λがai (i=1,2,3)と平行,すなわち,biとも平行のとき,λ=ai=biまわりの回転を表す方向余弦行列Ci(θ)は次のようになる。  以上の数学的手段を利用して、実際のセンサが計測する座標系から,グランド座標への変換を考える。 |